Mennyi az annyi?
írta: joghurt, 9 hónapja
Most csak egy rövid rövid kiegészítést tennék múltkori GNSS-es írásomhoz, számszerűleg mire számítsunk, ha telefonnal vagy sportórával megyünk futni.
A helyszín a Városliget, ahol a gumiburkolatú futókör hossza pontosan 2000 méter. (Lemértem rendesen.) A kör egy részén nyitott, egy részén fákkal közepesen takart, de magas házak közötti szűk utcák sehol sincsenek – azaz viszonylag jó a kilátás a műholdakra. És egy pontosan georeferált ortofotón (azaz nem műholdképen, hanem légifotón) nagyon jó felbontással látszik a futókör.
Versenyzőink egy nadrágzsebben vitt Redmi mobiltelefon [egysávos vevővel], egy Garmin epix (Gen2) Sapphire [L1/L5 vevő], illetve a jól megszokott uBlox C00-F9P [L1/L5 vevő RTK korrekcióval]. Ez utóbbival mentettem nyomvonalat FloatRTK fixszel (azaz amikor a vevő nem tudott pontos geometriai megoldást számolni), és "rendes" RTK fixszel is.
Az egyből látszik, hogy a mobil [fekete] a szokásos pontosságot (?) hozza: jóval odébb van, és ide-oda ugrálnak a pontok. Mind oldalirányban, mind menetirányban, pedig egyenletes tempóval futok.
A Garmin óra [kék] lényegesen jobb. Az egyik kör szinte teljesen a pályán belül maradt. A pontatlanabb körnél is szemlátomást működik valamilyen beépített szűrés, ami elsimítja a nyomvonalat.
A FloatRTK [bíbor] végig követi a pálya nyomvonalát, azon belül halad, különösebb cikkcakkok és hullámok nélkül. Legfeljebb az abszolút pontosságra lehet panaszunk.
És végül az RTK [zöld] végig pontosan ott megy, ahol futottam: a pálya jobb szélén. Ekkora felbontásban nem is lehet megkülönböztetni a három vonalat, annyira egymásra esnek. Rá is nagyítottam az alábbi képen. Igen, az ortofotó rasztere 10 cm. Tehát az egyes körök kb. 5 centin belül vannak. Már amennyire én tudtam pontosan ugyanott billegni.

Na jó, de jöjjön a lényeg: mit mutatnak a számok? Az alábbi táblázatban foglaltam össze az körök átlagos hosszát és a szintkülönbséget az egyes vevők szerint.
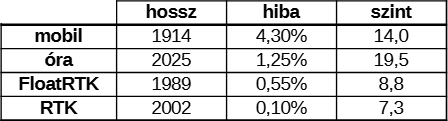
A tanulság annyi, hogy bár a mobilos nyomvonalak szörnyen néznek ki, és az abszolút pontosság is gáz a maga 20 méteres elcsúszásával (más alkalmakkor más irányba), a mért távolság nem ennyire durva, hanem egészen vállalható. És a távolság hibája lehet negatív is, valószínűleg az íveket jobban levágva.
Még egy érdekességet figyelhetünk meg: a pozíciómérés pontatlansága miatt az egymás utáni bogyók közötti távolság is óriási ingadozásokat mutat, az egyenletes tempó ellenére. Ha ebből számolnánk a sebességet, a sétálás és a világcsúcs között ingadozna egyik pontról a másikra. Szerencsére a GNSS vevők nem ezt teszik, hanem a Doppler-elv alapján mérik a sebességet, ami jóval pontosabb, és mentes az ugrándozós hibáktól.
Mivel a helymeghatározás elsősorban a 2D pozíciónkra fókuszál, a matekból az jön ki, hogy a függőleges pontosság kb. a vízszintes fele (azaz kétszer akkora a bizonytalansága).


